CHRIS KWOK

Sep 29, 2020

块编辑器

解析文本缩进父子关系还原深度优先遍历算法

在写块编辑器的时候需要处理一个将粘贴的文本根据缩进关系转换为带有级联父子（兄弟）关系的（多种类型）块。如何根据缩进识别解析块编辑器中的父子关系？还原深度优先遍历算法解析的数据结构。

从深度优先遍历开始

给定简易树形数据结构如：

const tree = {
  value: "root",
  children: [
    {
      value: "1",
      children: [
        {
          value: "1-1",
          children: [
            {
              value: "1-1-1",
              children: [],
            },
          ],
        },
      ],
    },
    {
      value: "2",
      children: [
        {
          value: "2-1",
          children: [],
        },
      ],
    },
    {
      value: "3",
      children: [
        {
          value: "3-1",
          children: [],
        },
      ],
    },
  ],
};

如果以深度优先算法来递归遍历平铺这个树：

function flat(tree, res = []) {
  res.push(tree);

  if (tree.children.length) {
    tree.children.forEach((data) => res.push(...flat(data)));
  }

  return res;
}

将树深度优先遍历平铺后得到一个扁平 List：

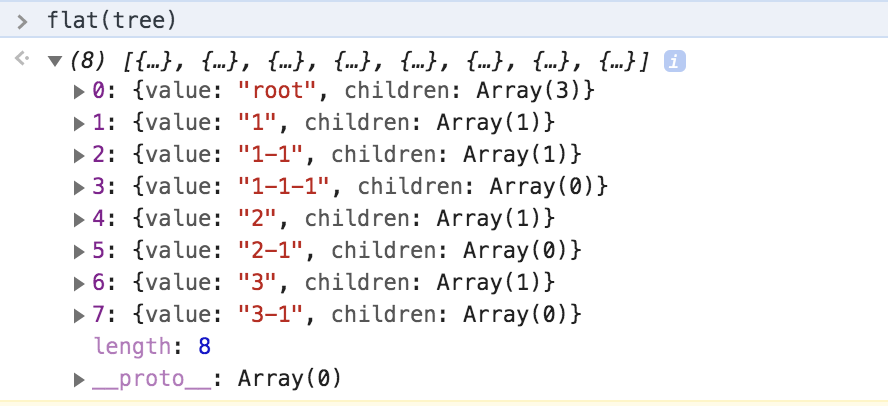
WX20200929-135709@2x.png

块编辑器的级联关系

块编辑器的块（任意类型）与块之间都可能存在的父子级联关系，在块操作的时候仍旧保持原有级联关系

如果粘贴一段文本在块编辑器中，会根据这段文本的不同行的缩进关系来生成对应的块的父子（兄弟）关系，如何做到这一点？

这其实就是将扁平的数据结构通过以缩进的空格来作为标杆转换为树形结构，恰巧由于上下文是紧密联系的关系，这个转换的过程正好相当于将原本树形结构以深度优先递归遍历出来的扁平数据结构还原为树。

所以关键在于记录这个缩进关系（通过对相邻两项缩进的空格数量进行对比来判断彼此关系）。

还原算法的关键点

不断对比相邻两项的空格数来确定相邻两项的级联关系
如何保证对比的临界值（平铺的同级根节点会有多个，相邻根节点就是对应的索引就是临界）
为了方便查找元数据的每一项实现给每一条数据添加 unique id

倒序复原深度优先遍历数据结构

需要注意的是还原深度优先的数据结构使用前先翻转使用方便正确查找插入；同时通过这个还原之后得到的结构时逆序的所以需要翻转整个 List：

// 1.
formatController(....reverse())
// 2.
loop(...).reverse()

具体实现过程：

const formatController = (_reverseArray) => {
  function loop(reverseArray) {
    // 遍历的过程不断的从原List截取数据放到Tree中
    // 保持原List备份
    const loopArray = reverseArray.slice(0);
    // 每次对比只需要考虑还没有比较过的根节点
    // pointer记录当前从哪里开始比较
    let pointer = 0;

    // 借助while只要pointer在原List索引范围内则继续查找
    while (pointer < loopArray.length) {
      // 获取当前索引所在数据
      const pointerData = loopArray[pointer];
      // 标识符 判断是否当前查询的元素存在子元素（缩进数大于当前项）
      let findSubordinates;
      // 正在遍历的对象
      let current;
      // 从外部记录的索引开始
      let k = pointer;

      for (; k < loopArray.length; k++) {
        current = loopArray[k];

        // 由于还原深度 接受的List经过倒序处理过
        // 判断current.tabSize < pointerData.tabSize 而非 current.tabSize > pointerData.tabSize
        // 判断是其子元素则将当前索引指向的数据推入当前项子元素List中
        // 同时从原List移除
        if (current.tabSize < pointerData.tabSize) {
          // 当前索引
          reverseArray.splice(
            reverseArray.findIndex(({ id }) => id === pointerData.id),
            1,
          );

          current.children = current.children || [];
          current.children.unshift(pointerData);

          // 代表当次循环找到子元素
          // 中断此次查找
          // 索引位置不变 开启下次查找
          findSubordinates = true;

          break;
        }
      }

      if (findSubordinates) {
        loop(reverseArray);

        break;
      }

      // 未查找到子元素 索引自增开启下一轮查找
      pointer++;
    }

    return reverseArray;
  }

  return loop(_reverseArray).reverse();
};

剪贴板文本：

格式化：

const format = string => string.split(/\n+/).map(text => ({
  text,
  tabSize: /^( )+/.exec(text)?.[0]?.length,
  children: [],
  // id: uuid.generate(),
}))
const flatTree = format(...).reverse()

// output:
// [
// 	{ text: ' 5', tabSize: 2, id: 'ifDrcusVgaNJGRWem3fFVS', children: [] },
// 	{ text: '4', tabSize: 0, id: 'p8BEPrFAdFtfiKm6mfeTcc', children: [] },
// 	{ text: '3', tabSize: 0, id: '9GqDaxK67ToLNQcPQjmKvK', children: [] },
// 	{ text: '    2-1-2', tabSize: 4, id: 'jG8prFHP9tXgbJSoqCYbki', children: [] },
// 	{ text: '    2-1-1', tabSize: 4, id: 'rvevchHuysMgAuDkzcr6ej', children: [] },
// 	{ text: '  2-1', tabSize: 2, id: 'wF4sAFnVT7enhx8efEvGNB', children: [] },
// 	{ text: '2', tabSize: 0, id: 'w2cXb6ojkvEMm7tz3r1Qui', children: [] },
// 	{ text: '1', tabSize: 0, id: 'nJCwvvptZuDAtiSCz9DjtL', children: [] }
// ]

最终调用 formatController(flatTree) 得到树形结构:

[
  {
    text: "4",
    tabSize: 0,
    id: "p8BEPrFAdFtfiKm6mfeTcc",
    children: [
      { text: "  5", tabSize: 2, id: "ifDrcusVgaNJGRWem3fFVS", children: [] },
    ],
  },
  { text: "3", tabSize: 0, id: "9GqDaxK67ToLNQcPQjmKvK", children: [] },
  {
    text: "2",
    tabSize: 0,
    id: "w2cXb6ojkvEMm7tz3r1Qui",
    children: [
      {
        text: "  2-1",
        tabSize: 2,
        id: "wF4sAFnVT7enhx8efEvGNB",
        children: [
          {
            text: "    2-1-1",
            tabSize: 4,
            id: "rvevchHuysMgAuDkzcr6ej",
            children: [],
          },
          {
            text: "    2-1-2",
            tabSize: 4,
            id: "jG8prFHP9tXgbJSoqCYbki",
            children: [],
          },
        ],
      },
      { text: "  2-2", tabSize: 2, id: "j6eUAMJdD2PqhfZLVEs5nS", children: [] },
    ],
  },
  { text: "1", tabSize: 0, id: "nJCwvvptZuDAtiSCz9DjtL", children: [] },
];

树形结构就很容易在业务中使用了（递归渲染级联关系）。写后端导出数据为 Markdown 文件时正好是将数据库级联字段深度优先遍历出来进行字符串的拼接以及写入文件；而将外部文件导入或者通过剪贴板粘贴时候又是将扁平字符串转为树形结构。

一饮一啄

👾

Published on Sep 29, 2020

Editor