所谓“搏一搏，单车变摩托”，很多时候我们以为的以‘小’博大其实并不小。

概率的认知偏差

中学时代的我一度是个刺头。曾经在课堂上回答老师问题的时候说过“我会做这题的概率和我中彩票的概率一样都是百分之五十，无非会或不会，中或不中”。而我中彩票的的可能却又几乎为零，所以我不会做这一题好像也没那么难堪，还借此刁难了老师，当时的老师也没给我一个令人比较认可的解释。

若不论其中的谬误，即使现在问一个人任意的概率问题，均能以是非两种答案概括，那么问题出在了哪里？

投掷十次硬币真的会有五次朝上吗

投掷十次硬币真的会有五次朝上吗？正常人都可以分辨，这是不一定的。那么如果问题是 “投递两次硬币出现一次正面朝上的概率是多大”？

统计学的规律只有经过了大量随机试验才能得出，也才有意义。但是随机试验得到的结果，和我们用古典概率算出来的结论可能是两回事。不仅掷十次硬币大部分时候不可能得到五次正面朝上的结果，你做其它随机试验也是如此。

掷十次硬币，正面朝上的次数应该是五次。但是如果真的拿一个硬币去试试，你会发现可能只有三次正面朝上，也可能四次正面朝上，甚至会出现没有一次正面朝上的情况。 如果把从零次正面朝上，到十次全是正面朝上的可能性都算出来，得到如下二项分布曲线：

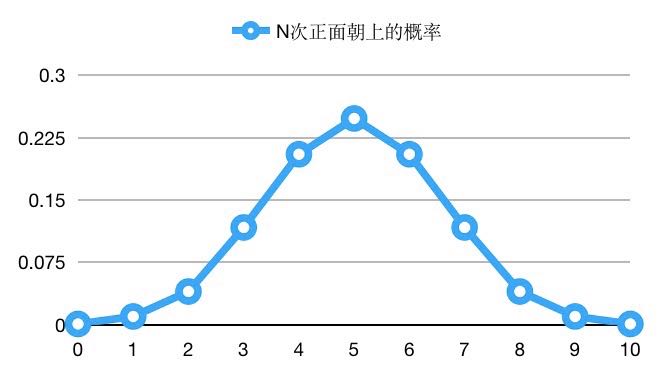
虽然出现五次正面朝上的概率最大，但是概率也只是在 0.25(0.246) 左右。

实验次数太少会导致随机性太大，而这导致很多人存在主观认知偏差，都明白其中的原因确在主观上忽略了这一点。

期望/方差/标准差

通俗理解期望就是出现结果的平均值，若设定每次实验的到期望的结果的概率是 P，投递硬币的次数为 N 次，那么平均值即数学期望值为：

E = P * N

对于投掷硬币的实验中每次正面朝上的概率为 1/2 时实验 N 次对应的期望即为 E = N / 2，如投掷十次硬币正反面朝上的的期望值均是 5。

而方差就是对由于实验充满随机性时对于错误结果误差的一种衡量，如投掷十次硬币出现正面朝上的次数是 3 次，那么误差就是平均值与结果的差值为 2。 如果把所有可能的误差考虑在一起进行加权平均（与期望值的差平方后取所有试验次数的平均值）处理后得到的“均差”就是平方差，简称方差。

s^2 = ((e1 - E)^2 + (e2 - E)^2 + ... + (en - E)^2) / n

由于方差是使用平方差值后计算平均数那么所谓标准差就是对方差进行开根处理后的返回值。

试验的次数越多，方差和标准差越小，概率的分布越往平均值 N * P 的位置集中。 在这种情况下事件 A 发生的次数，除以试验次数 N，当作事件 A 发生的概率，就比较准确。 反之试验的次数越少，概率分布的曲线就越平，也就是说事件 A 发生多少次的可能性都存在，这时你用事件 A 发生的次数，除以试验次数N，当作A发生的概率，误差可能会很大。

具体到抛硬币的试验，进行 100 次试验，标准差大约是 5 次，也就是误差相比平均值 50 大约是 10%。但是如果我们做 10000 次试验，标准差大约只有 50，因此和平均值相比，降到了 1% 左右。

你买彩票一定会中奖时要买多少次

计算发生的概率公式：

P = 1 - ((1 - K)^n)

上面提出的“投递两次硬币出现一次正面朝上的概率是多大”？由于正反概率都是 1/2, n 次实验概率相同那么存在 1 - (1 - 1 / 2)^2 = 3/4。

生活中很多人觉得某件事有 1/N 发生的概率，只要他做 N 次，就会有一次发生，这只是理想。 事实上，越是小概率事件理想和现实的差距越大。比如说一件事发生的概率为 1%，虽然进行 100 次试验后它的数学期望值达到了 1，但是这时它的标准差大约也是 1，也就是说误差大约是 100%，因此试了 100 次下来，可能一次也没有成功。

如果你想确保获得一次成功怎么办呢？你大约要四百次以上的试验，才能尽量确保发生。就是越是小概率事件，你如果想确保它发生，需要试验的次数比理想的次数越要多得多。

比如买彩票这种事情。你中奖的概率是一百万分之一，你如果要想确保成功一次，令 1 - ((1 - 1/1000000)^n) = 1 恐怕要买四百万次彩票的彩票才能使得中奖的概率接近 99%。即使中一回大奖，花的钱要远比获得的多得多。

远离赌博。

此外提高单次成功率要远比多做试验更重要。假如有 50% 的成功可能性，基本上尝试 4 次就能确保成功一次，当然理想状态是尝试两次。为了保险起见，要多做 100% 的工作。但是如果你只有 5% 的成功可能性，大约需要 50 次才能确保成功一次，而不是理想状态中的 20 次。为了保险起见，要多做 150% 的工作。

很多人喜欢赌小概率事件，觉得它成本低，大不了多来几次，其实由于误差的作用，要确保小概率事件发生，成本要比确保大概率事件的发生高得多。